하나의 문제를 해결하기 위한 다양한 알고리즘 중 가장 효율성이 좋은 것을 선택하기 위해서는 알고리즘의 수행시간, 차지하는 기억 공간 등의 비용으로 판단합니다.
복잡도( Complexity:O(n) )
알고리즘 수행 시 필요한 시간 또는 공간 비용
1. 시간 복잡도 (Time Complexity)
- 프로그램이 수행되는 시간
2. 공간 복잡도 (Space Complexity)
- 프로그램이 차지하는 기억 공간
f(n) = O(g(n)) f , g: 음수값을 갖지 않는 함수
알고리즘은 복잡도가 낮을수록 효율적입니다. 즉, 수행 시간이 짧거나 기억 공간을 적게 사용하는 알고리즘이 효율적이라고 할 수 있습니다. 그런데 최근 하드웨어 기술의 발달로 기억장치에 대한 비용이 줄어 기억 공간보다는 수행 시간에 단축에 대해 더 고려하고 있습니다. 그래서 일반적으로 복잡도는 시간 복잡도를 의미하게 됩니다.
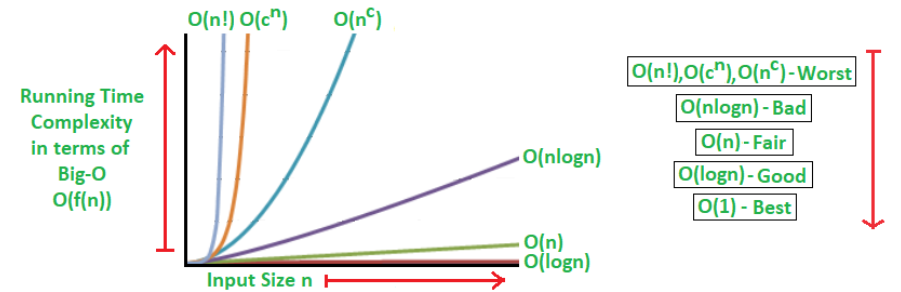
알고리즘의 복잡도는 'Big-O 표기법'을 사용하는데 복잡도 f(n) = O(g(n))는 "f(n)은 g(n)의 차수"라고 읽습니다.
이 복잡도는 f(n)은 n ≥ n0 인 모든 자연수 n을 입력으로 하는 알고리즘이 수행될 때, 그 수행시간이 f(n) ≥ c * g(n)이 되는 양의 정수 c와 n이 존재하면 성립하는 공식으로 알고리즘이 n개의 입력으로 수행될 때, 그 수행 시간이 |g(n)|에 양의 정수 c를 곱한 것보다 같거나 작은지를 확인하면 됩니다.
'컴퓨터공학 > 알고리즘 기초' 카테고리의 다른 글
| [알고리즘 이야기] 고전과 현대의 분할 정복 전략 (0) | 2020.08.12 |
|---|---|
| [알고리즘 이야기] 오일러 (0) | 2020.08.11 |
| [알고리즘 기초] 알고리즘의 복잡도 (0) | 2019.11.08 |
| [알고리즘 기초] 알고리즘의 표현 (0) | 2019.11.07 |
| [알고리즘 기초] 알고리즘이란? (0) | 2019.11.05 |