Studyenthusiast

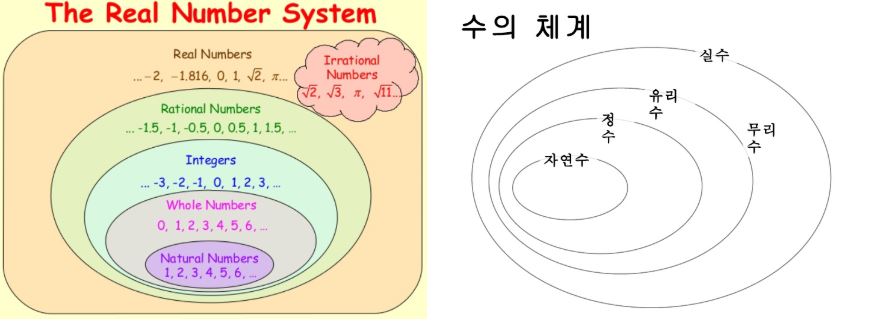
3. 유리수 (Rational Number: Q)

​

a, b ∈ Z(정수), a

* 하한항 (lowest)

- 분모와 분자 사이에 1이외의 공약수가 존재하지 않는 유리수

앞서 걸명한 정수 또한 유리수에 속합니다. 양의 정수 2는 2/1로 표현할 수 있고, 여기서 1과 2는 정수이며 분모 1이 0이 아니므로 유리수입니다.

유리수는 같은 값을 다양하게 표현할 수 있습니다. 유리수 6 / 27 은 2 / 9와 같고, 유리수 12 / 24는 1 / 2과 같습니다. 이 경우 6 / 27이나 12 / 24는 분자와 분모 사이에 1 이외의 공약수가 존재합니다. 6 / 27은 1 / 3이, 12 / 25는 1, 2, 3, 4, 6, 12가 공약수입니다. 

이렇게 분자와 분모 사이에 1 이외의 공약수가 존재하면 하한항이 아닙니다. 분자와 분모를 최대 공약수로 약분하면 하한항이 되는데, 6 / 27은 2 / 9가 12 / 24는 1 / 2이 하한항입니다.

ex) 다음 유리수가 하한항인지 확인하여 하한항이 아니면 하한항으로 만들어라

1) 25 / 70은 최대 공약수 5를 갖습니다.

그러므로 하한항이 아닙니다. 최대 공약수 5로 분모와 분자를 나누어 하한항을 만들면 5 / 14가 됩니다.

2,3) 7 / 10에서 7과 10, 9 / 14에서 9와 14는 1 이외의 공약수를 갖지 않습니다. (그러므로 하한항입니다.)

4) 32 / 50에서 32와 50은 최대 공약수 2를 갖습니다.

그러므로 하한항이 아닙니다. 최대공약수 2로 분모와 분자를 나누어 하한항을 만들면 16 / 25가 됩니다.

2. 정수 (Integer: Z)

양의 정수, 0 , 음의 정수로 구성된 수 체계

0은 양의 정수나 음의 정수에 속하지 않는 중립 원소로 기호가 붙지 않습니다. 반면, 양의 정수는 앞에 + 기호가 붙거나 생략된 0보다 큰 수이고, 음의 정수는 - 기호가 붙는 0보다 작은 수입니다.

ex) 절댓값 |28|을 갖는 정수를 모두 표현하라

절댓값이 |28|인 정수는 +28과 -28입니다.

1. 자연수 (Natural Number: N)

0보다 큰 양의 정수

n, b ∈ N 이고, b > 1, 0 ≤ ai < b 일 때

(b: 기수 / Cardinal Number , K: 자릿수 / positional number)

ex) 자연수 58910을 기수와 자릿수를 이용하여 표현

58910 = 5 * 10^2 + 8 * 10^1 + 10^0

이산수학에서 이산(Discrete)이라는 말은 연속성이 전혀 없는 분리된 상태를 말합니다. 즉, 이산수학은 실수(Real Number)와 같이 연속적인 성질을 가진 값에 대해 공부하는 것이 아니라, 정수(integer)와 같이 분리된 값에 대해 공부하는 학문입니다.

​

이렇게 분리된 값을 다룬다는 것은 컴퓨터의 특징과 밀접한 관련성을 가지고 있습니다. 예를 들면 컴퓨터는 0과 1의 분리된 값으로 모든 데이터를 표현하고 연산 및 처리를 합니다. 또한 컴퓨터에 적용되는 다양한 프로그램의 논리는 참과 거짓이 분명해야 하며, 그 프로그램이 처리하는 데이터들 또한 특정 집합의 원소로 정의되어 있어야만 합니다.

​

구조적 프로그램의 가장 대표적인 개념인 함수의 경우, 입력과 출력의 관계가 분명해야만 처리할 수 있습니다. 이와 같이 컴퓨터에 적용되는 많은 개념들은 이산적(Discrete)인 개념을 포함하고 있고, 이산수학은 명제나 논리의 참과 거짓, 집합의 포함, 관계의 유무, 함수의 입출력 등과 같이 확실하게 분리되는 개념을 다룹니다.

​

이산수학에서 다루는 개념들은 컴퓨터 명령 설계부터 입력 처리, 결과 출력까지 컴퓨터의 모든 과정을 이해하는 데 기본이 됩니다. 따라서 컴퓨터를 이해하기 위해서는 이산수학을 공부해야 합니다. 또한, 컴퓨터 프로그램 명령어 혹은 컴퓨터 자료의 표현이 모두 수학적인 개념에서 시작 되었습니다.