

일찍이 기원전 300년경에 그리스 수학자 유클리드(Euclid)가 제시한 이 알고리즘은 두 개의 수의 최대 공약수를 구하는 절차입니다. 조금 더 구체적으로 표현하자면 유클리드 알고리즘은 반복 절차입니다. 이 말은 즉, 결과에 도달할 때까지 동일한 수학적 연산이 계속 반복되는 것입니다.
예제로 a=1513과 b=357의 최대공약수를 구해보겠습니다. 먼저, 큰 수를 작은 수로 나눌 때 나오는 나머지 r₁을 알아내야 합니다. 이 예제에서는 r₁은 85입니다.
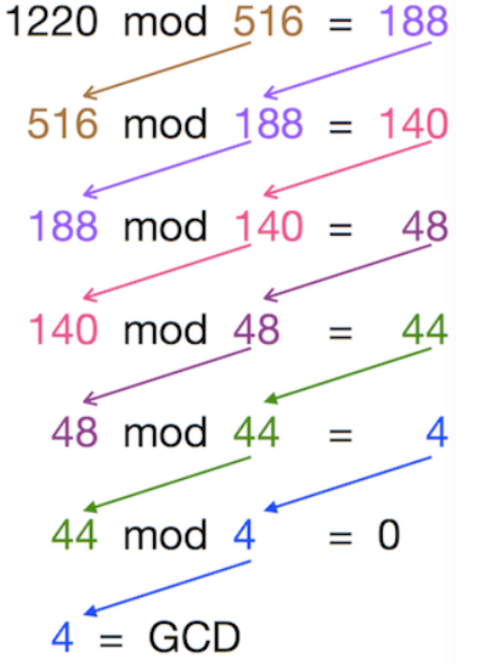
1513= 4 * 357 + 85
이번에는 작은 수 b를 r₁으로 나눌 때 나오는 r₂를 구합니다.
357 = 4 * 85 + 17
이러한 작업을 계속 반복하게 됩니다. 항상 작은 수(이 단계에서는 r₁)를 나머지 (r₂)로 나누는데, 나눗셈의 나머지가 0이 될 때까지 이 작업을 반복하게 됩니다. 이 예에서는 벌써 다음 단계에서 나머지가 0을 가지게 됩니다.
85 = 5 * 17 + 0
17은 앞서 등장한 모든 나머지들의 약수이며 a와 b의 약수이기도 합니다. 정확히 말하자면 17은 a와 b의 최대공약수입니다.
유클리드 알고리즘은 두 수를 우선 소인수분해한 다음에 그 소인수들을 비교하는 방법보다 더 신속하고 깔끔하게 최대 공약수 구하기 문제를 해결할 수 있습니다. 게다가 유클리드 알고리즘은 정수가 아닌 수에도 적용할 수 있습니다. 임의의 수들의 "공통 단위"를 유클리드 알고리즘으로 구할 수 있습니다. 하지만 이 알고리즘이 항상 유한한 개수의 단계를 거쳐 최종 결과에 도달하는 것은 아닙니다. 1과 √2에 유클리드 알고리즘을 적용하면, 나머지들이 점점 더 작아지기는 하지만
나눗셈의 나머지가 0으로 되는 일은 끝내 일어나지 않을 것입니다. √2처럼 통약불가능한 수들이 존재한다는 깨달음은 온 세계를 자연수들의 비율로 기술할 수 있다는 피타고라스 추종자들의 세계관을 무너뜨렸습니다.
※ 오늘은 '유클리드 알고리즘'에 대하여 알아보았습니다.
이 포스트는 학부에서 제공하는 기본적인 강의와 컴퓨터 공학 책들을 토대로 알기 쉽게 내용을 작성하였습니다. 하지만 계속 더 유익하고 논문 및 전문 서적을 읽어가며 더 추가돼야 할 내용이 있으면 알고리즘 포스트와 콘텐츠들을 계속 고도화하는 방식으로 진행하려고 합니다.
'컴퓨터공학 > 알고리즘 종류' 카테고리의 다른 글
| [알고리즘] 다중격자 알고리즘 (Multigrid algorithm) (0) | 2019.09.28 |
|---|