
이 단계는 실험의 배치와 실험 순서의 랜덤화를 선택하는 단계이며, 사전에 실험 계획에 해당되는 처음 3 단계들이 올바르게 이루어질 경우 비교적 쉽게 수행됩니다.
실험 설계의 선택 과정에는 샘플의 크기(반복 횟수)를 고려하고 적절한 실험 순서를 선택하는 것, 그리고 블록화 또는 랜덤화 조건(또는 제한)들의 포함 여부를 결정하는 것 등이 포함됩니다.
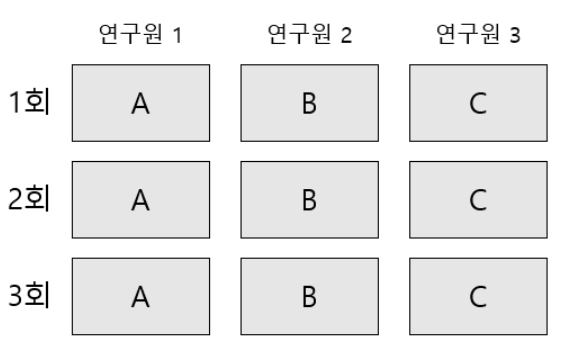
예를 들어 어떤 연구실에서 윤활유의 점도 차이를 조사하는 실험을 실시하였다고 가정합니다. 시중에 판매 중인 3개의 회사의 제품 A, B, C를 각각 3개씩 랜덤하게 취하고, 3명의 연구원(1, 2 ,3)에게 한 종류씩을 배당하여 총 9회 실험을 위의 그림과 같이 실시하였습니다. 이때 실험 결과는 각 연구원의 검사 능력에 영향을 받는다고 합니다.
이 실험에서 각 제품 간 점도차를 검정할 경우를 생각해보았을 때, 이 경우 각 제품간에 점도차가 없다는 귀무가설이 기각되더라도 그 원인이 각 회사에서 판매하는 윤활유간의 점도 차이라고 판단하기는 어렵습니다. 왜냐하면 이것은 연구원의 검사 능력에도 영향을 받기 때문입니다.

즉, 제품간에 나타나는 점도차이와 연구원간에 나타나는 검사 능력의 차이라는 두 효과가 서로 뒤섞여 구분할 수 없게 됩니다. 따라서 이러한 실험 설계는 적절한 방법이 되지 못합니다. 이러한 문제점을 해결하기 위해서는 각 연구원의 검사 능력의 차이가 모든 제품에 고루 영향을 주도록 평준화되어 나타나게 해야 하는데, 각 연구원마다 3가지 종류의 제품을 고르게 검사해보는 방법을 취하면 됩니다. 그러면 위의 그림과 같이 연구원 별로 하나의 블록을 설정하고 각 블록에 검사할 시료들을 동일하게 배당한다면 각 블록 내 환경이 동일해지고 각 블록간의 비교가 가능해집니다.
이 실험에서 각 회가의 제품간의 점도차가 없다는 귀무가설이 기각되었다면 그것은 각 회사에서 판매하는 윤활유간의 점도 차이에 기인한 것으로 판단할 수 있습니다. 이러한 실험 설계는 난괴법에 해당됩니다.

만일, 이와 같은 실험이 각 연구당 하루에 한 번씩 3이레 걸쳐서 이루어지고, 또 검사한 날짜에 따라 검사 결과가 영향을 받는다면 실험 날짜를 하나의 인자로 잡아주어 위의 그림과 같은 실험으로 설계될 수 있습니다.
그러나 이를 잘 살펴보면 첫날에는 B가 1회, C가 2회, 둘째 날에는 A가 2회, B가 1회, 셋째 날에는 각각 1회씩 실험되어 각 실험 날짜에 따라 동일한 빈도로 시료들이 실험되지 않았음을 알 수 있습니다. 이와 같은 실험은 날짜에 따른 효과가 실험 결과에 어느 정도 영향을 줄 수 있어서 적절할지 못합니다.
따라서 실험에서 고려되는 2가지 요인, 즉 연구원과 날짜에 따라 각 회사의 제품들(시료)이 고르게 배당되는 방법이 보다 합리적이라 할 수 있습니다.

위의 그림과 같은 설계는 이러한 요구를 만족시켜주는 실험 날짜와 연구원간의 각 조합에 한번씩 동일한 빈도로 사료(제품)가 배당되고 있음을 확인할 수 있습니다. 이렇게 하면 두 요인의 효과가 전체 실험 처리에 평준화 되어 실험 목적으로 채택한 반응특성치인 제품간의 점도 차이에 영향을 미치지 않게 됩니다. 위의 그림과 같은 실험 설계를 라틴방격 실험이라고 합니다.
이처럼 실험 설계의 선택은 실험 환경과 실험 목적에 따라 가장 적절한 배치 방법을 찾아가는 것이 중요하며, 실험 환경의 균일성이 확보되도록 해야 합니다.
'산업공학 > 실험계획법' 카테고리의 다른 글
| [실험 계획법] 데이터의 통계적 분석 (0) | 2019.10.24 |
|---|---|
| [실험 계획법] 실험의 실시 (0) | 2019.10.24 |
| [실험 계획법] 인자 및 수준의 선택 (0) | 2019.10.23 |
| [실험 계획법] 반응특성치 선택 (0) | 2019.10.22 |
| [실험 계획법] 문제의 인식과 제시 (0) | 2019.10.22 |